The Role of Biology, Chemistry, and Physics and the Secrets of Nature
To uncover nature’s secrets of nature, we must first establish how to observe it.
The study of mathematics begins with finding motifs through the observation of nature. The components of nature each reveal their unique properties through these motifs. To be a subject of study in mathematics, it must be represented as an image; and to become an image, motifs must be identified through observation. Those who meticulously observe living organisms, identify motifs, and illustrate them as images are known as biologists.
Once we have found a motif, now we need to find a pattern, which is a group of motifs. However, nature does not easily reveal its patterns. That is why mathematicians devised numbers and letters. People usually think that numbers are tools for counting, and symbols are tools for setting up equations. However, it is not as simple as we think. If each observed pattern could be assigned a number or letter, the patterns, which are the collection of motifs, become clearly defined. In other words, numbers and letters serve as mathematical tools that play an important role in identifying patterns within motifs. If we identify the patterns in nature, we can understand its structure. Patterns are relational expressions woven from numbers and symbols, and these form chemical formulas. The structure of nature is a fractal shape.
To uncover the secrets of nature, it is important to understand the structure of nature, represented by fractals.
Chemists are people who name visible forms through chemical formulas. However, there are countless things in this world that possess names, even though they lack physical forms. Mathematicians are the people who continually strive to assign names to things without forms. Merely discovering patterns does not mean we have fully grasped the secrets of nature. Within nature's patterns, countless other patterns exist, and, at the same time, patterns also collapse. People need a higher level of awareness to perceive these elements clearly at a glance. Moreover, we must also consider the aspect of time since patterns are confined within the spaces of nature.
To find the regularities of nature, one must be able to understand space as it moves with time. Unlike the static concept of patterns, regularity possesses continuity that unfolds over time. So, how exactly can we find the regularities of nature? How can we uncover the hidden order within the seemingly irregular, non-linear structures of the world of physics? Living organisms all strive to maintain their complete form. To do so, they must possess some kind of internal force and hidden laws. The world that physicists deal with is this kind of chaos.
Mathematics Uses Letters, Arithmetic Does Not
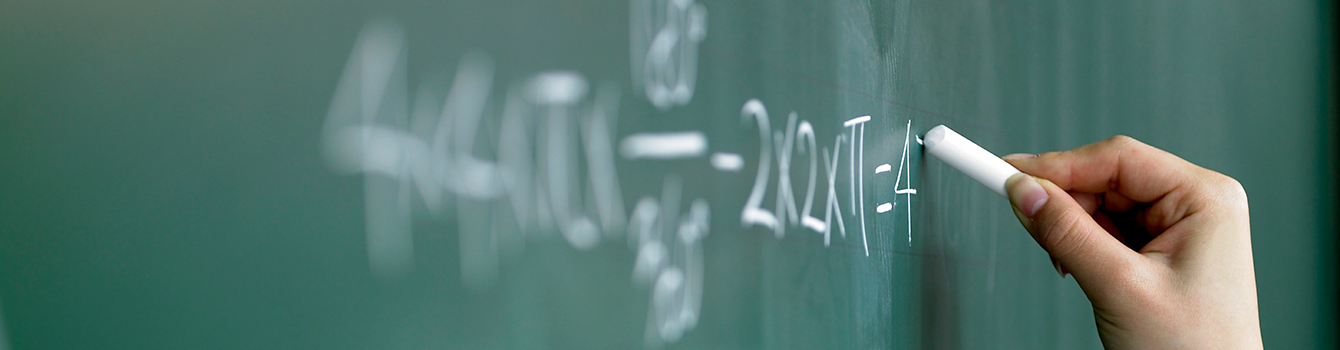
Many people tend to think that arithmetic and mathematics are the same. Before exploring the difference between the two, it is necessary to first understand what algebra is. Algebra is a branch of mathematics that studies the relationships between numbers using letters instead of numerals. At first glance, arithmetic does not seem all that different from algebra. In arithmetic, it is impossible to handle numbers generally because there are no symbols to represent concepts like "a certain number," "an unknown number," or "a number that can be any value." However, in algebra, letters such as a, b, and c are used instead of specific numbers, which allows greater flexibility than in arithmetic.
For example, let’s look at “5+3=3+5.” By replacing 5 with 𝑎 and 3 with 𝑏, we can express this as the algebraic expression “𝑎+𝑏=𝑏+𝑎.” At this point, any numbers can be substituted for 𝑎 and 𝑏, allowing algebra to represent all possible cases with a single expression. In other words, while arithmetic can only express specific situations, algebra enables the representation of general situations.
Applying the same principle allows problems to be easily solved by communicating solutions simply and clearly to people using letters. This is why it is said that the use of letters made mathematics more approachable. To summarize, arithmetic studies individual facts, while mathematics studies general principles. The distinguishing factor between the two is the use of letters.
The use of letters in mathematics means that one can concretely represent the structure of nature. If the collection of motifs, known as a pattern, is not visible even after drawing the images of motifs, one can understand the importance of attaching numbers or letters to each motif.
Patterns and Pattern Collapse
The observation of nature and drawing it, followed by assigning numbers and letters, does not always guarantee the discovery of patterns. Furthermore, even if a pattern is discovered, it is not always possible to definitively say that the pattern represents the essence of the phenomenon. Since patterns and pattern collapses occur simultaneously in the nature we live in, we must be able to recognize patterns and pattern collapses at a glance to understand the essence of phenomena.
For example, when we look at the surface of a lake, we can observe that gentle ripples appear in a regular pattern. However, when a leaf suddenly falls onto the surface, concentric waves spread out from that point. The introduction of a new pattern causes the original ripple pattern to collapse. If the wind begins to blow here as well, the pattern collapse will continue, making it increasingly difficult to discern any rules. If patterns and pattern collapses can occur in something as simple as ripples, how many patterns and pattern collapses might be happening within living organisms?
Even if biologists and chemists have depicted the forms of nature as images, it is very rare for patterns to be readily apparent. It is dangerous to conclude that a pattern does not exist simply because it is not visible. Nature possesses a mathematical structure of higher dimensions that is difficult for human senses and reason to grasp.
If a pattern is not easily visible, we should examine the image by attaching letters or numbers. Mathematics is the study that uncovers the secrets of nature. Numbers and letters are the tools of mathematicians for uncovering the secrets of nature, that is, finding patterns. As the saying goes, “The use of letters made mathematics convenient, and the concept of speed made mathematics great.” In this way, numbers and letters serve as tools for mathematicians to uncover the secrets of nature, forming the foundation of idealism.
An Ideal Mathematics Education and Curriculum
Mathematics is the study that uncovers the secrets of nature.
To uncover the secrets of nature, one must first find motifs through observation of nature (the world of biology), then understand the fractal structure of nature (the world of chemistry), and finally grasp the world of chaos, which consists of invisible forces and laws (the world of physics).



What role does mathematics, the pinnacle of natural sciences, play in biology, chemistry, and physics?
Nature exhibits a structural relationship between the world of chemistry, represented by fractals, and the world of physics, represented by chaos. All living organisms in nature maintain such interrelationships, and mathematics is the study that predicts how all these natural components will be generated in the future and how they will eventually disappear and vanish.
Creating a prediction program through mathematics means uncovering the secrets of the life and death of living organisms. Finding patterns in nature enables such predictions. If we can uncover the secrets of nature, we can create something that will make people happy. That is why mathematics is the foundational technology of all advanced industries. If the desirable mathematics education is realized through a series of practices that uncover the secrets of nature, it can preserve the future of a nation.
Therefore, the chapters included in the mathematics textbooks for all grade levels should be organized and structured according to the principles of the desirable mathematics education.
Advanced industrial technology encompasses all aspects that have the potential to enhance human happiness. The advanced technologies available to each country supply the essential resources needed to ensure a secure future. Consequently, the mathematical capabilities of a nation serve as a key indicator of its overall competitiveness. Therefore, mathematics education must be properly established to preserve the future of a nation.

